VisualisationMétro est GI-complet

Les InformationArchitects sont partis d'une carte du métro de Tokyo pour proposer une visualisation intéressante des sites web les plus connus ou les plus tendance. Est-ce qu'il est facile de programmer un logiciel qui ferait un travail similaire avec d'autres données, d'autres cartes de métro ? Plus précisément, qu'en est-il de la complexité théorique de ce problème, qu'on appellera VisualisationMétro ?

Formalisons un peu le problème tout d'abord. Disons qu'on a une liste quelconque de termes (de sites web par exemple), une liste quelconque de thèmes qu'ont certains de ces termes en commun, ainsi qu'un plan de métros. VisualisationMétro consiste à déterminer s'il existe algorithme polynomial (c'est à dire que le temps de déroulement de l'algorithme sera proportionnel à un polynôme en la taille des deux listes) pour savoir si l'on peut étiqueter les stations de métro par la liste de termes, et chaque ligne de métro par un concept de telle sorte que deux termes partagent un même thème si et seulement si les deux stations correspondantes se trouvent sur la même ligne de métro.

Si vous trouvez une solution à ce problème, n'hésitez pas à me la communiquer ! En effet, VisualisationMétro est équivalent (plus précisément se réduit en temps polynomial) au problème d'isomorphisme de graphes : on a deux graphes (disons, de même taille n), c'est à dire des ensembles de "noeuds" numérotés de 1 à n dont certains sont reliés par des arêtes, et on veut savoir si on peut numéroter les noeuds du premier de telle sorte qu'il soit identique au deuxième. La complexité de ce problème est une question ouverte depuis plus de trente ans : on ne sait s'il est polynomial ou NP-complet (un problème NP-complet, on peut en donner une définition "économique" : vous serez millionnaire si vous trouvez un algorithme polynomial pour le résoudre, ou que vous montrez au contraire qu'il n'en existe pas. De façon plus intuitive c'est un problème qu'il est très long de résoudre de manière exacte avec un ordinateur). Pour avoir une idée des algorithmes utilisés en pratique pour résoudre efficacement un problème d'isomorphisme de graphes, lisez la synthèse (en anglais) de Scott Fortin : The Graph Isomorphism Problem.

Regardons de plus près la réduction de isomorphisme de graphes à VisualisationMétro. Déjà, on va montrer que le problème d'isomorphisme de graphes se rapporte au problème d'isomorphisme de graphes bipartis (l'ensemble de noeuds d'un graphe biparti peut être découpé en deux ensembles V1 et V2 tel qu'il n'y a aucune arête entre deux noeuds de V1 ou entre deux noeuds de V2). Pour cela, supposons qu'on a deux graphes G1 et G2, dont on veut savoir s'ils sont isomorphes (identiques à réétiquetage près, donc). Transformons chaque arête en deux arêtes un chemin constitué de deux arêtes consécutives : on obtient deux 2-subdivisions : G'1 et G'2... qui sont des graphes bipartis, et qui sont isomorphes si et seulement si G1 et G2 sont isomorphes ! Donc si on avait un algorithme polynomial pour savoir si G'1 est isomorphe ou pas à G'2, on saurait si G1 est isomorphe ou pas à G2.

Deuxième étape maintenant. Supposons qu'on a deux graphes bipartis G1 et G2, dont on veut savoir s'ils sont isomorphes, et qu'on connaît un algorithme pour résoudre VisualisationMétro. G1 et G2 étant des graphes bipartis, les sommets de G1 sont découpés en deux ensembles de sommets indépendants A1 et B1, on fait de même avec G2 pour obtenir A2 et B2. On crée alors la carte de métro suivante : les lignes de métro correspondent aux éléments de A1 et les stations aux éléments de B1, et pour tous les éléments de B1 reliés à un certain élément a de A1, les stations correspondant à ces éléments de B1 seront sur la ligne associée à a. Ensuite, on considère les éléments de A2 comme des termes, et ceux de B2 comme des thèmes et on exécute l'algorithme résolvant VisualisationMétro. On l'exécute une nouvelle fois en considérant A2 comme des thèmes, et B2 comme des termes. G1 et G2 sont isomorphes si et seulement si au moins une de ces deux exécutions montre qu'on peut faire correspondre les deux listes à la carte.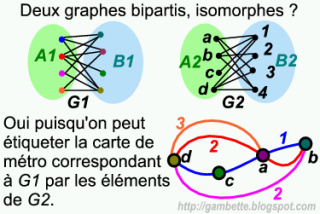

Alors évidemment, les InformationArchitects n'ont pas commencé par s'arracher les cheveux en se demandant s'ils étaient assurés de pouvoir placer leurs sites web et leurs thèmes sur une carte de métro, mais ils ont certainement procédé de façon heuristique, en trouvant une méthode (commencer par placer les noeuds de plus fort degré peut-être ?) pour être à peu près sûrs d'obtenir un résultat à peu près correct, à défaut d'être tout à fait exact. Par exemple, en comparant en détail avec la carte du métro de Tokyo, on remarque que certaines stations ont été oubliées. Ce qui ne change rien à l'intérêt de la visualisation, puisque les "petites stations" où ne passe qu'une ligne sont moins connues et identifiables au premier coup d'oeil que les "grandes" qui sont bien étiquetées par des noms de sites web. Et puisque la visualisation a un intérêt autre qu'esthétique plutôt pour ceux qui connaissent bien la carte de départ, y ont des repères, il pourrait être intéressant de faire ça sur la carte du métro parisien. A suivre...