Postures et énigme politicombinatoire
Avec les débats Royal-Bayrou demain et Royal-Sarkozy la semaine prochaine, on peut espérer que la campagne va toucher au fond des discours de chacun, après avoir plutôt touché le fond. La campagne du premier tour a été une succession de postures (et d'impostures ?).
Les trois candidats arrivés en tête ont tenu à incarner le politique nouveau, avec en particulier une liberté de ton rafraîchissante, à laquelle chacun a ajouté ses spécificités. Ségolène Royal s'est définie comme l'incarnation de l'ordre juste, de la femme, de la mère, du vote utile anti-Le Pen. Pour Nicolas Sarkozy, c'était la fermeté, la réforme ou rupture, et plus récemment le rassemblement. François Bayrou a commencé par être l'opposant aux puissances médiatiques, pour devenir le centriste en lutte contre le bipartisme, ou encore le vote utile anti-sarkozy.
Ces postures ont l'avantage d'être très faciles à médiatiser. Elles créent la polémique et peuvent facilement être démontées par les adversaires : les qualités mises en avant par le candidat sont retournées contre lui, ou tout simplement niées preuve à l'appui ou presque. Royal a donc subi le machisme et les accusations d'incompétence. Sarkozy est devenu un facho, ou l'héritier du bilan du gouvernement sortant. Bayrou, un utopiste sans majorité à l'assemblée profondément ancré à droite.
Le débat "proposition contre proposition" sur des questions précises n'a jamais été mis en avant à la télévision ou dans la presse écrite. Ce que j'aurais aimé avoir, ce n'est pas le catalogue de propositions de chacun des candidats, mais plutôt, sur chaque thème, les différents points de vue et les convergences. Des tentatives de synthèse ont été entreprises, mais elles ne faisaient pas apparaître clairement les consensus et les incompatibilités. C'est une démarche que j'aurais attendu de la part des centristes : combien de points du pacte présidentiel de Ségolène Royal seraient acceptés aussi par Nicolas Sarkozy ? On en a vu défiler, des pactes ou questionnaires (celui de Nicolas Hulot, du collectif AC Le Feu, des langues, le questionnaire sur les logiciels libres...) : ce sont devenus des packs de propositions ne donnant lieu à aucun débat contradictoire, aucun résumé synthétique.
Et les sites qui prétendaient avec une série d'une vingtaine de questions calculer votre similarité avec tous les candidats ? Où sont les tableaux des réponses des candidats à ces questions ? Pour une fois qu'on aurait pu avoir un avis clair (voire binaire) à des questions censées nous déterminer politiquement de la part de tous les prétendants...
On a préféré la politique spectacle, plus facile à "vendre", et plus ludique. Attention, je ne le critique pas totalement : déjà, ça a permis d'atteindre presque 85% de participation au premier tour. Je vais même plus loin, c'est l'appréciable, voire nécessaire, première étape d'une démarche qui me plaît : commencer par des légèretés pour motiver à "mettre les mains dans le cambouis". Exprimé par Stefan Zweig dans La Confusion des Sentiments : "celui qui n'est pas passionné devient tout au plus un pédagogue ; c'est toujours par l'intérieur qu'il faut aller aux choses, toujours, toujours en partant de la passion." Et si on a droit à de vrais débats de fond calmes et intéressants dans les jours qui viennent, après la passion de l'avant premier-tour, la campagne présidentielle de 2007 sera réussie !
Et maintenant à moi d'illustrer cette démarche, en motivant un problème combinatoire par une petite histoire de politique d'image et de posture : le Problème du Club de Réflexion, que j'appellerais presque le problème du siècle (issu d'une discussion initiée avec Nergal)...
F.B. affirme n'avoir pas parlé à N.S. depuis 3 ans. Ces deux hommes appartiennent à un même club de réflexion, qui se réunit tous les mois de la façon suivante : parmi tous ses n membres, un certain nombre est invité à venir manger à l'Automobile Club de France. Ils peuvent alors discuter autour de tables de k personnes. Disons qu'il y a t tables. En pratique il paraît que k=7, qu'environ 300 personnes participent à chaque dîner soit t=43, et que le club a environ n=700 membres. La première question, facile, consiste à déterminer quelle est la probabilité que F.B. n'ait en effet jamais dîné à la même table que N.S. depuis 3 ans, en supposant que les organisateurs des soirées invitent et placent leurs membres aléatoirement à chaque fois.
Calculons la probabilité à chaque réunion que F.B. ne soit pas à la même table que N.S. Est-ce que N.S. est là ? Il y a seulement tk invités, donc il n'est pas là avec proba (n-tk)/n. S'il est là, alors F.B. n'est pas là avec proba (n-tk)/(n-1), et il est là avec proba (tk-1)/(n-1). Si les deux sont là, alors une fois que N.S. est placé il y a k-1 chaises vides autour de lui, et il reste à placer tk-1 convives donc F.B. n'est pas à sa table avec proba (tk-k)/(tk-1). Comme on le voit avec l'arbre de toutes les possibilités ci dessous, on obtient la probabilité que F.B. ne soit pas à la table de N.S. à une réunion par la formule :
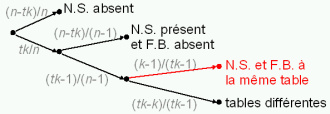
Soit pour les valeurs de n, t et k données une probabilité de 99,6309% que F.B. et N.S. ne se rencontrent pas à une certaine réunion. On élève à la puissance 36 pour chacune des 36 réunions en 3 ans : il y a 87,5% de chances qu'ils n'aient effectivement pas mangé à la même table pendant tout ce temps...
La deuxième question, beaucoup plus compliquée, consiste à trouver la stratégie de placement des organisateurs. On considère raisonnablement qu'ils veulent que tout le monde parle avec tout le monde. Quel est donc le nombre minimum de réunions à effectuer pour qu'en effet tout le monde ait mangé au moins une fois avec tout le monde ? Et comment inviter et placer les membres pour atteindre ce minimum ? En déduire le nombre maximal de réunions consécutives où N.S. et F.B. ne mangent pas à la même table.
 Si on prend la restriction de ce problème avec n=tk et k=2, ça revient à un problème d'organisation de tournoi d'échecs : on a n participants, et on fait jouer en parallèle t parties, en cherchant à minimiser le nombre de parties permettant que tout le monde ait joué contre tout le monde. Cela nous permet d'introduire de la théorie des graphes : on considère le graphe complet, c'est à dire qu'on relie un ensemble de 2k sommets (les joueurs) par toutes les arêtes possibles, chaque arête correspondant à une partie d'un joueur contre l'autre. On va colorier les arêtes de telle sorte que les couleurs correspondent à des parties qui peuvent se dérouler en parallèle, c'est à dire que deux arêtes partageant un même sommet n'auront pas la même couleur. On cherche à minimiser le nombre de couleurs, c'est à dire l'indice chromatique du graphe complet à 2k sommets. Le problème, classique ("promenade des demoiselles"), est résolu ici : 2k-1 couleurs (donc 2k-1 parties) suffisent, vous avez même la configuration des parties !
Si on prend la restriction de ce problème avec n=tk et k=2, ça revient à un problème d'organisation de tournoi d'échecs : on a n participants, et on fait jouer en parallèle t parties, en cherchant à minimiser le nombre de parties permettant que tout le monde ait joué contre tout le monde. Cela nous permet d'introduire de la théorie des graphes : on considère le graphe complet, c'est à dire qu'on relie un ensemble de 2k sommets (les joueurs) par toutes les arêtes possibles, chaque arête correspondant à une partie d'un joueur contre l'autre. On va colorier les arêtes de telle sorte que les couleurs correspondent à des parties qui peuvent se dérouler en parallèle, c'est à dire que deux arêtes partageant un même sommet n'auront pas la même couleur. On cherche à minimiser le nombre de couleurs, c'est à dire l'indice chromatique du graphe complet à 2k sommets. Le problème, classique ("promenade des demoiselles"), est résolu ici : 2k-1 couleurs (donc 2k-1 parties) suffisent, vous avez même la configuration des parties !Pour le cas général je cherche encore, quelques variantes du problème sont réunies sur cette page...








3 commentaires:
j'adore cette deuxième partie de billet comme il m'arrive par trop rarement d'en écrire.
Mon chouette dernier dans ce style, c'était celui là : l'usage des probabilités comme moyen de preuve... ;-)
Héhé marrant ton post en effet. Je bute tout de même sur le terme "preuves" : on n'est jamais à l'abri d'un problème de modélisation...
Bon et cette généralisation du "problème des demoiselles" elle t'inspire ?
Pour des tables de 3 personnes, les "Steiner Triple Systems" semblent résoudre le problème.
Enregistrer un commentaire